The calculation of water and gas flows in complex and heterogeneous media is central to technological solutions aimed at tackling current climate and energy challenges, such as the underground storage of CO2 or heat.
For calculations of this type, an adaptive model was developed by researchers at IFPEN and PoliMi1 in order to better incorporate the highly discontinuous nature of the underground environment. Collaboration between the two institutes is continuing with a view to improving the performance of these numerical simulations.
1 Polytechnic University of Milan
Irregular spatial distributions of porosity and permeability
Numerically simulating water and gas flow in a heterogeneous porous medium is very important for some new applications associated with climate/energy challenges, such as the underground storage of CO2 or of heat. The heterogeneities of the medium in question stem both from the diverse nature of the rocks and the presence of complex geological structures, such as channels and macropores: they are reflected in irregular spatial porosity and permeability distributions, as illustrated by the examples shown in figure 1.
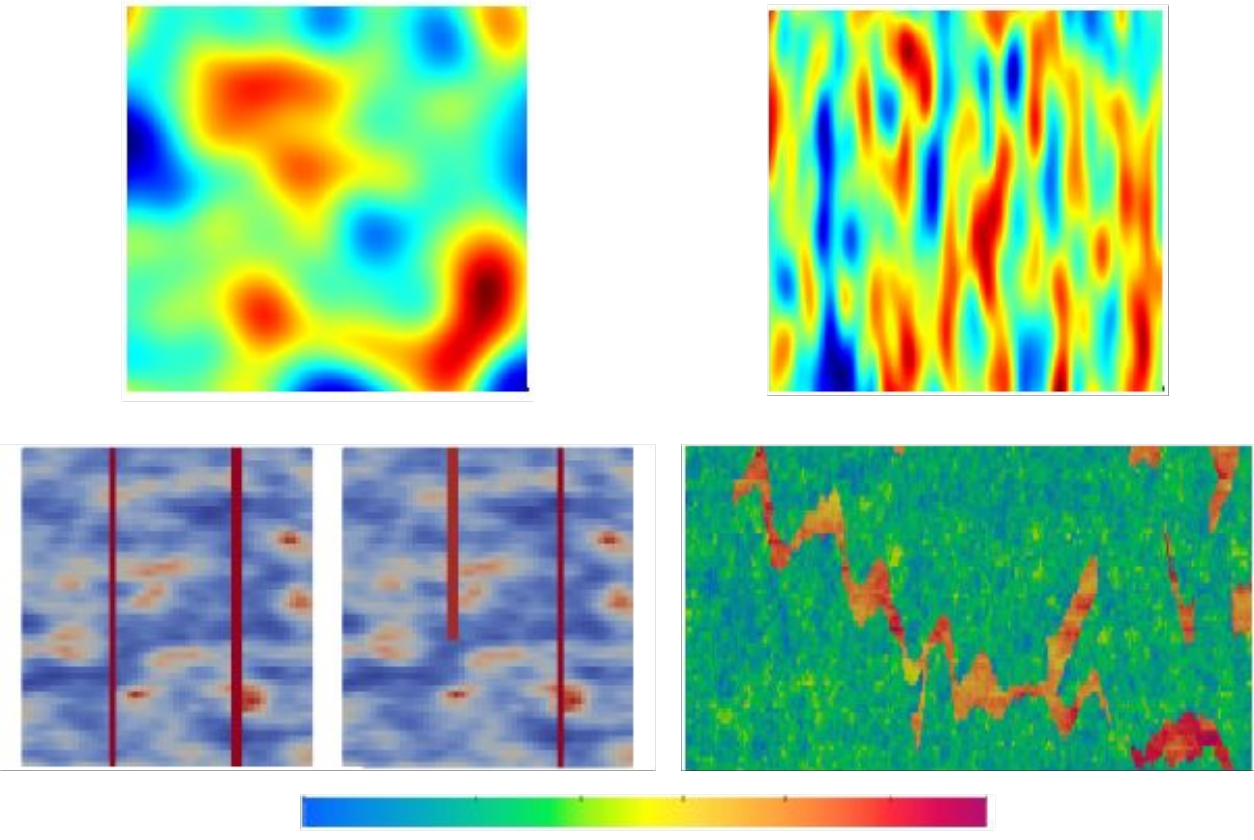
Top left: generated by an isotropic Gaussian distribution [3]
Top right: generated by an anisotropic Gaussian distribution [3]
Bottom left: generated by a Matérn distribution [3,4] with transverse macropores [4] represented by vertical red lines
Bottom right: measured on layer 35 of the SPE10 project implementation [5]
Darcy’s law and its limits
In terms of modeling, the choice of constitutive law relating the speed of fluid flow to the pressure gradient is crucial. Traditionally, Darcy’s law is used for the entire domain concerned by the simulation: it is linear, and therefore numerically inexpensive, and accurately describes low-speed flows. When these speeds increase, for example in highly permeable structures, linearity is no longer respected and Darcy’s law loses its relevance. Hence it has been demonstrated experimentally that it leads to an overestimation of the high speeds calculated [6,7]. In order to correct this effect, a quadratic term is commonly added to Darcy’s law, thus transforming it into Forchheimer’s law. This additional term incorporates inertia effects by increasing flow energy. However, due to the non-linearity thus introduced, the resolution of spatially discretized equations proves to be costly in terms of calculation time.*
Adoption of an adaptive model
To overcome this effect while minimizing the impact on the precision of results, researchers at IFPEN and PoliMi proposed an adaptive model [1,2] that only uses Forchheimer’s law where appropriate. Hence, for numerical resolution across the entire domain, the choice of law applied is made, for each iteration, as a function of a criterion based on physical measurements (such as domain permeability and fluid viscosity) relating to flow speed: if this exceeds the value of the criterion, Forchheimer’s law is used
Regularization of the adaptive problem
A major difficulty with this adaptive model resides in the discontinuities created when suddenly shifting from one law to another in so-called transition zones. These discontinuities have a significant impact on the mathematical formulation of the model and make it difficult to work with. To overcome this difficulty, IFPEN and PoliMi proposed a regularization of the adaptive model based on an averaging of the speeds in transition zones. The impact of moving between laws is thus smoothed out, thereby eliminating the detrimental discontinuity. In addition to the existence and uniqueness of the solutions for both approaches (“discontinuous” and “regularized” problems), researchers verified that they did indeed converge to the same one [1,2]. Figure 2 shows the domain partitioning for the SPE10 project from figure 1 for the case of the regularized model, for three distinct speed criterion values: the lower the criterion, the more extensive are the regions for which Forchheimer’s equation applies.

From left to right: decreasing speed criterion
Further efforts required to better predict calculation sub-regions
While the regularized model is continuous, it is nonetheless highly non-linear in the transition zones; as a result it can still be numerically costly to use. Partnership research is currently underway to further reduce the calculation time, using the regularized model as a predictor of “Darcy” and “Forchheimer” regions, in such a way as to enable the numerical simulation to be based directly on the law predicted in each region, without transition zones. Hence the discontinuity of the adaptive model and the excess non-linearity of the regularized model will be eliminated. The prediction step will exploit machine learning techniques, making prior assumptions about the simulation domain: geometry of the constituent regions, boundary conditions on pressure and velocity as the model’s input data.
References:
1. FUMAGALLI, A., PATACCHINI, F. S. (2022). Model adaptation for non-linear elliptic equations in mixed form: existence of solutions and numerical strategies. ESAIM: Mathematical Modelling and Numerical Analysis, 56(2), 565–592. DOI : https://doi.org/10.1051/m2an/2022016.
2. FUMAGALLI, A., PATACCHINI, F. S. (2022). Well-posedness and variational numerical scheme for an adaptive model in highly heterogeneous porous media. ArXiv 2206.07970. Lien arXiv : https://arxiv.org/abs/2206.07970.
3. PICHOT, G., LEGRAND, S., KERN, M., TEPAKBONG-TEMATIO, N. (2022). How to initialize the Circulant Embedding method to speed up the generation of stationary Gaussian Random Fields? HAL 03190252. Lien HAL : https://hal.inria.fr/hal-03190252.
4. WINTER, R., VALSAMIDOU, A., CLASS, H., FLEMISCH, B. (2022). A study on Darcy versus Forchheimer models for flow through heterogeneous landfills including macropores. Water, 14(4), 546. DOI : https://doi.org/10.3390/w14040546.
5. CHRISTIE M. A., BLUNT. M. J. (2001) Tenth SPE Comparative Solution Project: A Comparison of Upscaling Techniques. Society of Petroleum Engineers, Houston, Texas. DOI : https://doi.org/10.2118/66599-MS.
6. ZHANG, T., ZHAO, Y., GAN, Q., YUAN, L., ZHU, G., CAI, Y., CAO, B. (2018). Experimental investigation of Forchheimer coefficients for non-Darcy flow in conglomerate-confined aquifer. Geofluids, 1–21. DOI : https://doi.org/10.1155/2018/4209197.
7. SOBIESKI, W., TRYKOZKO, A. (2014). Darcy’s and Forchheimer’s laws in practice. Part 1. The experiment. Technical Sciences, 17(4), 321–335. Lien web : https://www.infona.pl/resource/bwmeta1.element.baztech-2757664d-c0fc-43c9-9c80-dc3a5f6572e9.
Scientific contact: Francesco Patacchini





