The Richards equation is used to simulate water flows in partially saturated soils. Its resolution is difficult in highly heterogeneous porous media where capillary pressure can strongly vary in space. A new methodology has been developed to improve the robustness and the accuracy of the calculations in these media.
Solving the Richards equation: what numerical challenges?
The Richards equation is a simplified flow model, frequently used in hydrogeology to simulate water flows in partially saturated soils. It is traditionally solved using a two-point finite-volume method. However, for some cases, the resulting system of non-linear equations turns out to be difficult to solve and the accuracy of the obtained solutions can be deteriorated when the capillary pressure law changes in space.
During the PhD work [1], researchers from IFPEN and Inria have proposed a new version of this discretization method, which is more robust and more precise with respect to the non-linearities. They have also established the existence and uniqueness of the discrete solution, as well as its convergence towards a solution of the variational problem.
Strong non-linearity and spatial discontinuity of capillary pressure
Capillary pressure is defined as the pressure difference existing at the interface between two phases, one considered to be wetting with respect to the porous rock and the other not. In the Richards formulation, these two phases correspond to water and air respectively. Assuming that the air pressure is constant, water pressure directly deduces from the capillary pressure, a measurement generally defined in the form of a non-linear function of the water saturation and also dependent on the type of the local rock (Figure 1). This latter dependency can also lead to water-saturation discontinuities and hence to water accumulations or suctions on the interfaces between two rock types (Figure 2). The accurate modeling of these phenomena is therefore important.
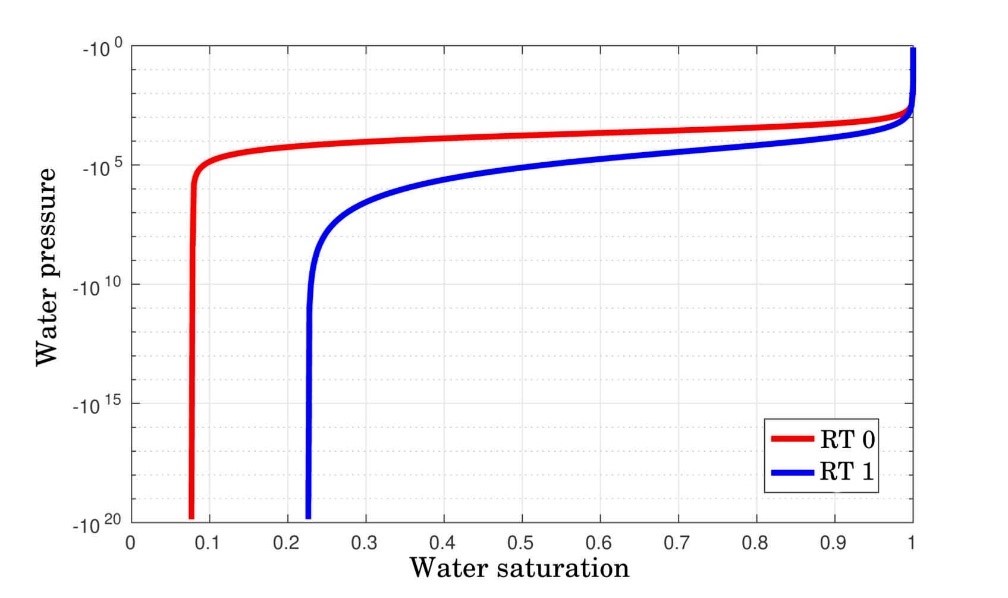
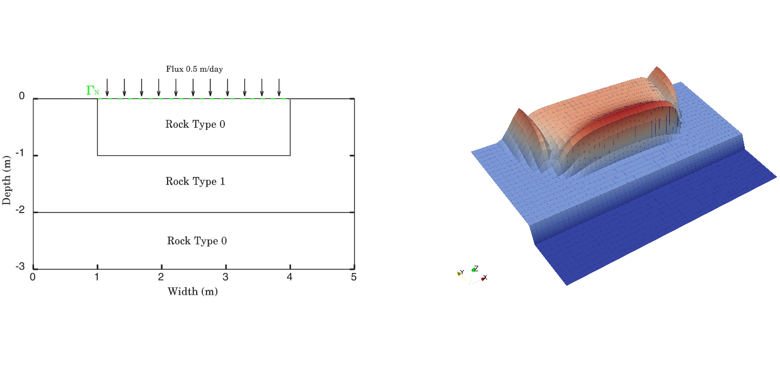
A parametrization technique to improve the convergence of Newton's algorithm
Because of the non-linearity of the law describing capillary pressure, Newton’s algorithm, which is used to solve the discrete system, can barely converge, or not at all. This pitfall can be avoided thanks to an appropriate and regular change of the variable during the iterations. That is the principle of the parametrization technique proposed in [2]. This previous work used the Kirchhoff transformation as a possible variable to be used in Newton’s algorithm. In practice this variable cannot always be calculated. The work done during this study has led to propose parametrizations that are directly based on water saturation and capillary pressure. These new parametrizations ensure a good convergence of the calculations with highly non-linear laws [3].
A simplified refinement for an increased accuracy on rock-change interfaces
The “two-point” finite-volume discretization is widely used in simulation softwares. But this resolution scheme is known to suffer from a lack of precision on interfaces presenting a change in the capillary-pressure law. A classical solution to improve its precision consists in adding unknowns on the faces between two rock types [4]. The research, conducted here, has also shown that the simple addition of two fine cells on each side of the rock interface makes it possible to numerically improve the convergence order of this scheme. In practice, this solution requires no change to an existing code. This solution has also been compared with other ones in a second study [5] and was shown to be the most appropriate one in the majority of the test cases.
A methodology with future applications
The proposed methodology can easily be extended to more general two-phase or three-phase flow models in porous media. This result will thus benefit other applications, such as the simulation of the underground storage of CO2. In particular, its use is planned within the ArcGeoSim computation platform which is developed by IFPEN in partnership with the CEA [6, 7].
References:
1. S. Bassetto, Towards more robust and accurate computations of capillary effects in the simulation of multiphase flows in porous media, PhD thesis Lille University (2021).
2. K. Brenner, C. Cancès, Improving Newton's method performance by parametrization: the case of Richards equation, SIAM J. Numer. Anal. 55 (2017), 1760-1785. https://hal.archives-ouvertes.fr/hal-01342386
3. S. Bassetto, C. Cancès, G. Enchéry, Q-H. Tran, Upstream mobility finite volumes for the Richards equation in heterogeneous domains, ESAIM : M2AN 55 (2021), 2101-2139. https://hal.archives-ouvertes.fr/hal-03109483
4. G. Enchéry, R. Eymard, A. Michel, Numerical approximation of a two-phase flow problem in a porous medium with discontinuous capillary forces, SIAM J. Numer. Anal. 43 (2006), 2402-2422. https://doi.org/10.1137/040602936
5. S. Bassetto, C. Cancès, G. Enchéry, Q-H. Tran, On several numerical strategies to solve Richards’ equation in heterogeneous media with finite volumes, preprint (2021). https://hal.archives-ouvertes.fr/hal-03259026
6. G. Grospellier, B. Lelandais, The Arcane development framework, Proceedings of the 8th workshop on Parallel/High-Performance Object-Oriented Scientific Computing 4 (2009), 1-11. https://doi.org/10.1145/1595655.1595659
7. https://github.com/arcaneframework/framework
8 . M.T. van Genuchten, A closed-form equation for predicting the hydraulic conductivity of unsaturated soils. Soil Sci. Soc. Amer. J 44 (1980) 892–898.
Scientific contact: Guillaume.Enchery@ifpen.fr





