Flow simulation in the underground environment involves complex multiphase mixtures in which phases can appear and disappear over time. To manage this complexity, several approaches were tested (unified formulation, non-parametric interior point method, etc.) within the framework of a PhD thesis. The new method employed is very robust and makes it possible to obtain good convergence of resolution algorithms.
Mixture phase management
In many underground simulators (CO2 storage, geothermal energy, reservoir), a challenging aspect concerns multiphase mixtures and, more specifically, the incorporation of thermodynamic equilibrium laws relating to the chemical species present. The difficulty resides in the management of the appearance and disappearance of phases for different components. The conventional dynamic approach, known as variable switching, consists in only keeping the unknowns of present phases and the associated equations. It is nevertheless cumbersome and expensive, to the extent that the action has to be carried out continuously, even from one iteration to another within a numerical resolution procedure, such as the conventional Newton algorithm.
The contribution of the unified formulation
An alternative approach, known as unified formulation and recently proposed by Lauser et al. [1], makes it possible to maintain a fixed set of unknowns and equations throughout the calculations. In terms of theory, this represents a significant advance that has since led to numerous research projects in the scientific calculation community. In terms of practice, however, the new formulation involves complementarity equations that are non-differentiable. As a result, it is necessary, after discretization, to use the semi-smooth Newton-min method, which does not guarantee convergence to a single solution. Hence the difficulty of the problem is transferred to the numerical resolution step but it has not disappeared.
Design of a non-parametric interior point method
To avoid abandoning the unified formulation approach midway through the process and exploit its potential to the full, a team of researchers from IFPEN and the INSA engineering school in Rennes decided to overcome this final obstacle. Within the framework of a jointly supervised thesis [2], they set about developing better adapted resolution algorithms, offering greater calculation convergence. The approach adopted consisted in drawing inspiration from tried and tested methods in the field of optimization under constraints and transposing them to general systems of equations (which do not necessarily come from an optimization problem). As a result, a non-parametric version1 of interior point methods2, called NPIPM, was proposed for algebraic systems. These methods are recognized for their considerable optimization efficiency [3].
1 “non-parametric” means that it is not necessary to have the regularization parameter that is used in interior point methods and is often their “weak link” tend to 0 “by hand”.
2 “interior” means that during the iterations, the unknown vector remains inside a region where the positivity constraints are strictly satisfied.
Analysis and extension of cubic equations of state
Another major contribution of the thesis [3] was the understanding and partial resolution of an additional obstruction to the efficiency of the unified formulation approach, hitherto not identified in the literature. This concerns the limitation of the field of definition of the Gibbs functions3 associated with cubic equations of state4 . To deal with the potential non-existence of any system solution, a natural extension of Gibbs functions was recommended. Similarly, a large number of previously unknown theoretical properties of the unified formulation were established [4]. The complementarity of these results with numerical aspects of the NPIPM method was tested as described below.
3 Gibbs free energy (free enthalpy) function G associated with the second principle of thermodynamics.
4 equation of state of a fluid that can be written as a third-degree polynomial as a function of volume.
Numerical comparison for several phase equilibrium models
In terms of robustness of convergence, the combination of the new NPIPM method with Gibbs function extension makes it possible to improve on the results obtained using the Newton-min method. For example, the red area on the left part of figure 1, in the concentrations space (c1, c2), highlights the states for which Newton-min diverges, for a given choice in terms of the calculation start point. On the right, with the same start point but with NPIPM, these problematic states have disappeared in the various field zones: liquid (green), gas (blue) two-phase (liquid-gas, cyan).
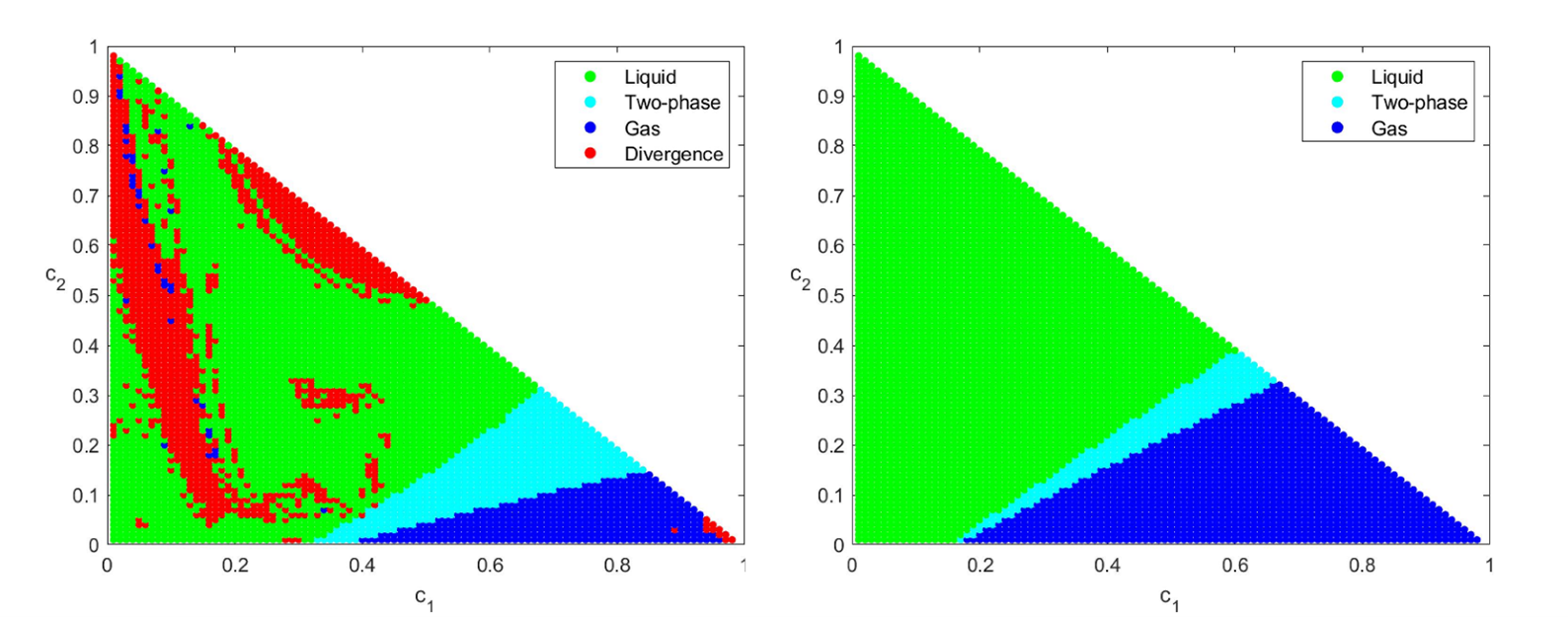
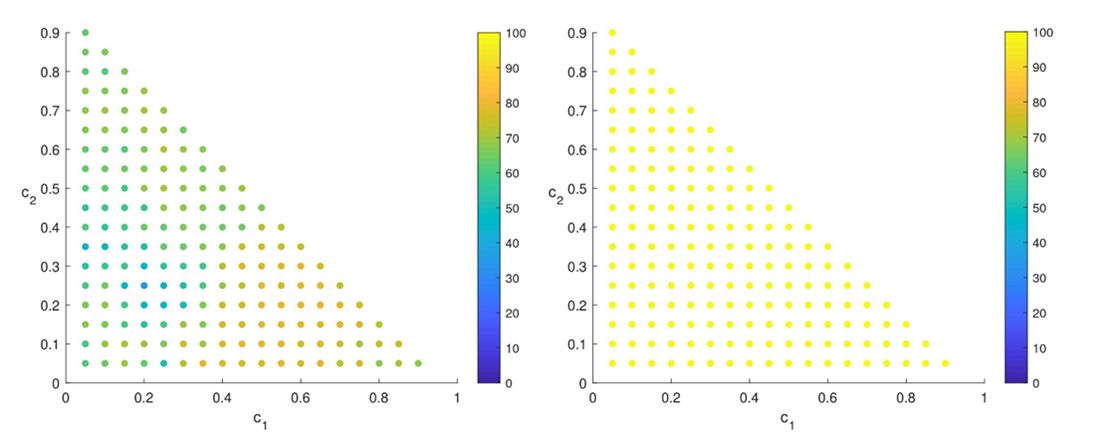
Figure 2 illustrates the advantage of the the new method in another way: it indicates the number of situations (start point) for which each of the two algorithms converges. It can be seen that NPIMP (right) obtains a score of 100% for all cases considered unlike Newton-min (left). For these numerical tests, we considered the Peng-Robinson cubic equation of state with extended Gibbs functions [5].
References:
[1] A. LAUSER, C. HAGER, R. HELMIG, B. WOHLMUTH, A new approach for phase transitions in miscible multiphase flow in porous media, Advances in Water Resources 34 (2011), pp. 957–966. https://doi.org/10.1016/j.advwatres.2011.04.021
[2] D. T. S. VU, Numerical resolution of algebraic systems with complementarity conditions. Applications to the thermodynamics of compositional multiphase mixtures, PhD thesis 2020UPASG006, Université Paris-Saclay, 2020. https://tel.archives-ouvertes.fr/tel-02987892
[3] M. H. WRIGHT, The interior-point revolution in optimization: history, recent developments, and lasting consequences, Bulletin of the American Mathematical Society 42 (2005), pp. 39–56. https://doi.org/10.1090/S0273-0979-04-01040-7
[4] I. BEN GHARBIA, M. HADDOU, Q. H. TRAN, D. T. S. VU, An analysis of the unified formulation for the equilibrium problem of compositional multiphase mixtures, ESAIM: M2AN 55 (2021), pp. 2981–3016. https://doi.org/10.1051/m2an/2021075
[5] D. T. S. VU, I. BEN GHARBIA, M. HADDOU, Q. H. TRAN, A new approach for solving nonlinear algebraic systems with complementarity conditions. Application to compositional multiphase equilibrium problem, Mathematics and Computers in Simulation 190 (2021), pp. 1243–1274. https://doi.org/10.1016/j.matcom.2021.07.015
Scientific contact : Ibtihel.Ben-Gharbia@ifpen.fr, Quang Huy Tran





