The hypothesis of elliptical particle motion of eigen body S-waves projected on a supposed common plane of elliptical polarization of any one of the eigen S-wave vectors S1, S2 associated to a given wave vector K has been developed in a previous academic work on Elastic shear wave anisotropy [1] (Eudier, 1988). This study was initiated in 1988 by Naville, as an attempt to define the theoretical relative shapes of particle motion of the transmitted eigen shear wave modes in order to simplify the detection of shear wave anisotropy by the appropriate signal processing of surface seismic and borehole seismic surveys. The measured multicomponent seismic signals constitute the observable displacements, velocities or accelerations described in the elasticity theory.
The ensuing results obtained in 1988 were not fully interpreted at the time.
Due to the symmetry of complex stress tensor (L. Landau & E. Lifchitz [2]) the simple convolution product of the eigen particle motion displacement vectors was found to be null: tS1*S2 = 0.
Note that the simple product is different from the Hermitian convolutive scalar product. This property leads to the expected observation of an elliptical particle motion running the SAME angular rotation (clockwise/CW, or anticlockwise/CCW), for the two S-wave eigen modes propagating into the same spatial direction.
In practice, the eventual ellipticity of the seismic particle motion has not been observed in a spatially consistent manner on single direct P-waves and direct S-waves recorded by the high quality, modern downhole VSP tools, characterized by their excellent mechanical coupling to the borehole wall, insuring the isotropy of their receiver response , called “ vector fidelity”.
In the addendum to the Eudier’s study, Naville illustrated a manner to change the linear system axes of the 2D Shear polarization plane into an elliptical vectorial coordinate system when designing the S-wave anisotropy detection computer process. However, questions were remaining about the physical signification of the additional parameters brought by the eventual ellipticity eigen S-wave modes, and about what happens to the shape of eigen S-waves when several fracture sets are present in a rock sample. Additionally, a singularity would occur when the ellipticity increases so much that the two eigen modes become circular with an identical angular rotation, and merge! Last, it was noted that the eventual presence of elliptical eigen S-modes would express a difference of orientation of the linear eigen directions of the symmetrical real part of the stiffness tensor in comparison with the symmetrical imaginary part of the same complex tensor, which would be difficult to explain physically .
Around 2010, after having analyzed many field VSP datasets and after second thoughts, the author suggests that the identical angular rotation of the two eigen S-wave modes of propagation represents an unrealistic idea, lacking any support by observations.
Consequently, the shape of particle motions of the eigen waveforms S1 and S2 projected on an initially supposed elliptical polarization plane of S1, both degenerate into orthogonal linear motions, in the plane orthogonal to the wave vector K in a homogeneous anisotropic viscoelastic propagation medium; this phenomenon is called “ordinary birefringence“ by L. Landau & E. Lifchitz [2].
An additional argument refers to the shape of an elliptical S-wave incident after normal incidence reflection onto a perfectly isotropic reflecting plane, i.e. a total reflector with a reflection coefficient equal to unity (perfect mirror). In the attached file entitled Elliptical Shear wave reflection [3], the reflected elliptical S-wave is seen to keep the same elliptical shape motion (wiggle signal time response) with the same angular rotation as the incident signal, although propagating into the exact opposite spatial direction.
Therefore, in an anisotropic medium, an isotropic total reflector plane orthogonal ray path or group velocity direction of the incident S-wave reverse the propagation direction along the same incident ray path, even where the ray orientation slightly deviates from the normal to the elliptic S-wave polarization plane in the anisotropic medium.
The normal to the reflected S-wave polarization plane is symmetrical of the normal to the incident S-polarization plane relatively to the reflector plane, or locally tangent to the reflecting surface.
The identity of the angular rotation of a hypothesized elliptical wave motion of an eigen S-wave for the back and forth propagation along the same given ray path looks unrealistic because it violates the principle of symmetry of spatial propagation, as illustrated on figure 1.
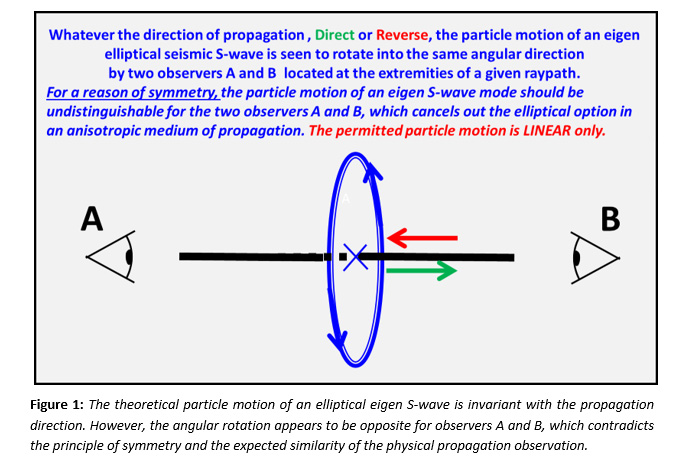
Conclusions
In a homogeneous anisotropic and attenuating viscoelastic medium, and for any spatial ray path or group velocity vector, the particle motions of the P and S transmitted body wave eigen modes are linear; they might not always be mutually orthogonal to each other, by a small angle, but they remain linearly polarized. Surface waves are not considered here.
Although the direction of the P-wave particle motion may not coincide with the direction of the propagation vector K in an anisotropic medium, it may also deviate by a few degrees from the direction of group velocity vector, or ray path (ref: S. Crampin [4], 1982, Fig.1 ).
Consequently, the linear direction of the eigen vectors of the stiffness tensor coincide spatially with the linear directions of the eigen vector of the symmetric attenuation/dissipation tensor.
Linear polarization of P-waves is commonly observed on 3 component VSP datasets recorded over large volumes of homogeneous and attenuating rock formations drilled by numerous boreholes worldwide. Observations of ultrasonic P and S waves eigen linear polarization are largely reported too, often exhibiting two principal S-waves with significantly different velocities and significantly different attenuations in homogeneous anisotropic core samples.
By chance, the linear polarization of seismic body waves observed in all experimental studies and industrial surveys over a very large frequency range, from earthquake and seismic low frequencies up to ultrasonic high frequencies, help refine theoretical details of the S-wave propagation and birefringence in the homogeneous viscoelastic domains of the earth subsurface.
The elliptical polarization of inhomogeneous body waves, as described by R.D. Bordcherdt-73 [5] and R.D. Bordcherdt-86 [6], is not evidenced by industrial and academic observations. Would this hypothetical ellipticity possibly be too small to be identified coherently over significantly long distance of propagation on VSP surveys? The modern instruments of the whole chain of VSP acquisition and processing have greatly contributed to improve the precision of the seismic wave propagation and properties since the 1980’s.
Therefore, the linear polarization of eigen modes of seismic waves transmitted through a homogeneous medium of anisotropic velocities and anisotropic attenuations is the only one retained. This simplifies the understanding of acoustic anisotropy of rocks and facilitates the interpretation of measurements, for the benefit of various subsurface exploration practitioners.
|
Scientific contact: |
References:
- Elastic shear wave anisotropy / F. Eudier (ENS - Ecole Normale Supérieure de Lyon) - Anisotropie des ondes de cisaillement élastiques L'Anisotropie et les Phénomènes d'Atténuation. Effets sur les ondes ultrasonores. Application à la Prospection Pétrolière (Addenda en anglais)
>> Rapport de stage de Diplôme d'Etudes Approfondies d'Acoustique physique (DEA), Paris, 1988.
- L. Landau & E. Lifchitz / Théorie de l’élasticité, Editions Mir, 1967.
>> https://archive.org/details/landau-lifchitz-physique-theorique-vol-07-theorie-de-lelasticite-mir-1967
- Elliptical Shear wave reflection / C. Naville (IFPEN) - Réflexion d'onde de cisaillement elliptique. Mode propre elliptique d'onde de cisaillement après réflexion en incidence normale sur une interface isotrope, propagée dans un milieu homogène.
>> Note 2022.
- S. Crampin / Stuart Crampin, Ralph A. Stephen, Robert McGonigle - The polarization of P-waves in anisotropic media, Geophysical Journal International, Volume 68, Issue 2, February 1982, Pages 477–485
>> https://doi.org/10.1111/j.1365-246X.1982.tb04910.x
- R.D. Borcherdt-73 / Energy and plane waves in linear viscoelastic media, Journal Geophysical Research, 78, (N°14), 2442-2456.
>> https://doi.org/10.1029/JB078i014p02442
- R.D. Borcherdt-86 / Borcherdt,R.D., G. Glassmoyer, L. Wennerberg, 1986: Influence of welded boundaries in anelastic media on energy flow, and characteristics of P, S-I, and S-II waves: Observational evidence for inhomogeneous body waves in low-loss solids, Journal Geophysical Research, 91, 11,503-11,518
>> https://doi.org/10.1029/JB091iB11p11503





