A numerical recipe for adapting the landscape map

The climate is changing and it is doing so too fast. The impacts on our environment are already visible in many regions of the world.  In such a context, it is important to understand the dynamics of our environment in order to construct tools capable of anticipating the risks stemming from this climate disruption.  Among these tools, numerical models offer a very effective solution for testing a wide range of climate scenarios, taking into account numerous physical, chemical and biological processes. 

For example, numerical landscape evolution models are widely used in order to understand and quantify the relationship between the climate and the hydro-sedimentary dynamics of a water catchment area. Two ingredients are required to construct models of this type: a “good ladleful” of a water flow model and a “large cup” of sedimentary transport, all bound together by the pooled expertise of geoscientists and applied mathematicians! This recipe formed the foundation for the Dionisos software solution [1], which became DionisosFlow [2], designed for the purposes of modeling hydro-sedimentary processes.

A base ingredient: “numerical consistency”

One of the “sensitive” aspects of these models, which have been known for over 20 years, is a much greater dependence on mesh size and shape¹ than can usually be attributed to the simple numerical discretization of our continuous equations.  For a long time, the origin of this dependence remained unclear. In 2020, a first article [2] was published identifying one of the reasons for which some water flow models conventionally used by the community produced an artificial mesh dependence. The reason turned out to be simple: the flow algorithm, which was supposed to mimic an “empirical” model, was in reality entirely consistent with established physics, namely a Manning-Strickler model². However, these algorithms had not been explicitly designed to reproduce established physics, expressible through a set of partial differential equations. And since chance does not always get things quite right, it turns out that the algorithms required a few tweaks to ensure this was the case. These tweaks are referred to as “numerical consistency”. Without it, an algorithm is bereft of its physics: it still models something, but something completely artificial!  This defect, present in historical models, can now be corrected for most embedded algorithms [3].

¹ A numerical domain being made up of a set of elementary meshes
² An empirical formula used to estimate the average velocity of a liquid flowing in a conduit with ^{a free surface, i.e., flowing in a conduit that does not completely enclose the fluid or in an open channel.}

An essential utensil: a filter to remove lumps

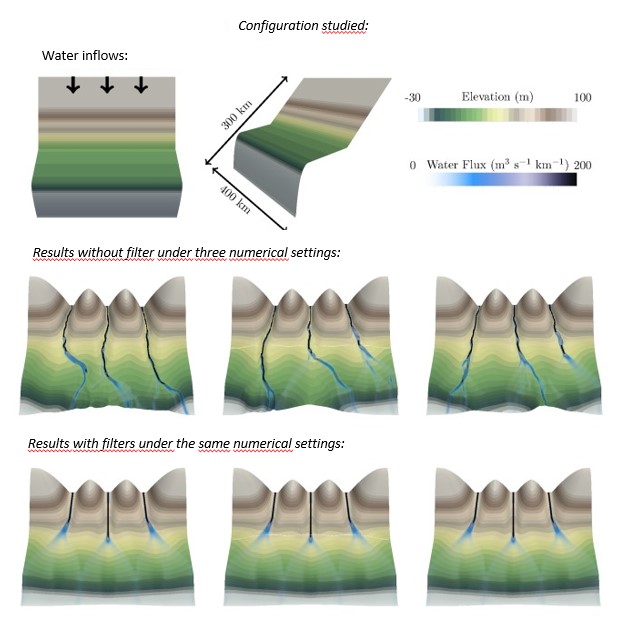
However, solving this problem is not enough to avoid “lumps” (those tiny flaws in the numerical solution which, when amplified, spoil the dish!) in landscape evolution models. The other aspect that needs to be considered is the coupling between water flow and sediment transport. To do this, we set about adapting an approach commonly deployed in LES³-type models to eliminate the “lumps” arising from turbulence below a certain size [4]. In practical terms, this boils down, on the one hand, to water flowing through a filtered topography and, on the other hand, only sediments transported by a filtered water network impacting the topography. The key ingredient is known as the Leray-alpha⁴ filter: as well as fulfilling the desired function, it has the distinction of preserving the non-linear effects associated with flow-transport coupling, while filtering out numerical noise⁵.

³ Large Eddy Simulation : méthode de modélisation de la turbulence utilisée dans le domaine de la dynamique des fluides
⁴ Regularization method by local averaging of alpha size
⁵ Solution errors associated with the numerical resolution process

Reproducible results from one simulation to the next

The benefits of such a method became clear when it was realized that the reproducibility of results was not guaranteed in its absence. This occurred, for example, when the problem was solved with different solvers for the same simulation, or indeed simply when the number of processors involved in solving the numerical system was varied. The results obtained were then considerably altered (a river, instead of flowing straight ahead, could randomly fork), but this has now been resolved thanks to the use of the filter (Figure 1).

With the right proportions, the dish is ready 

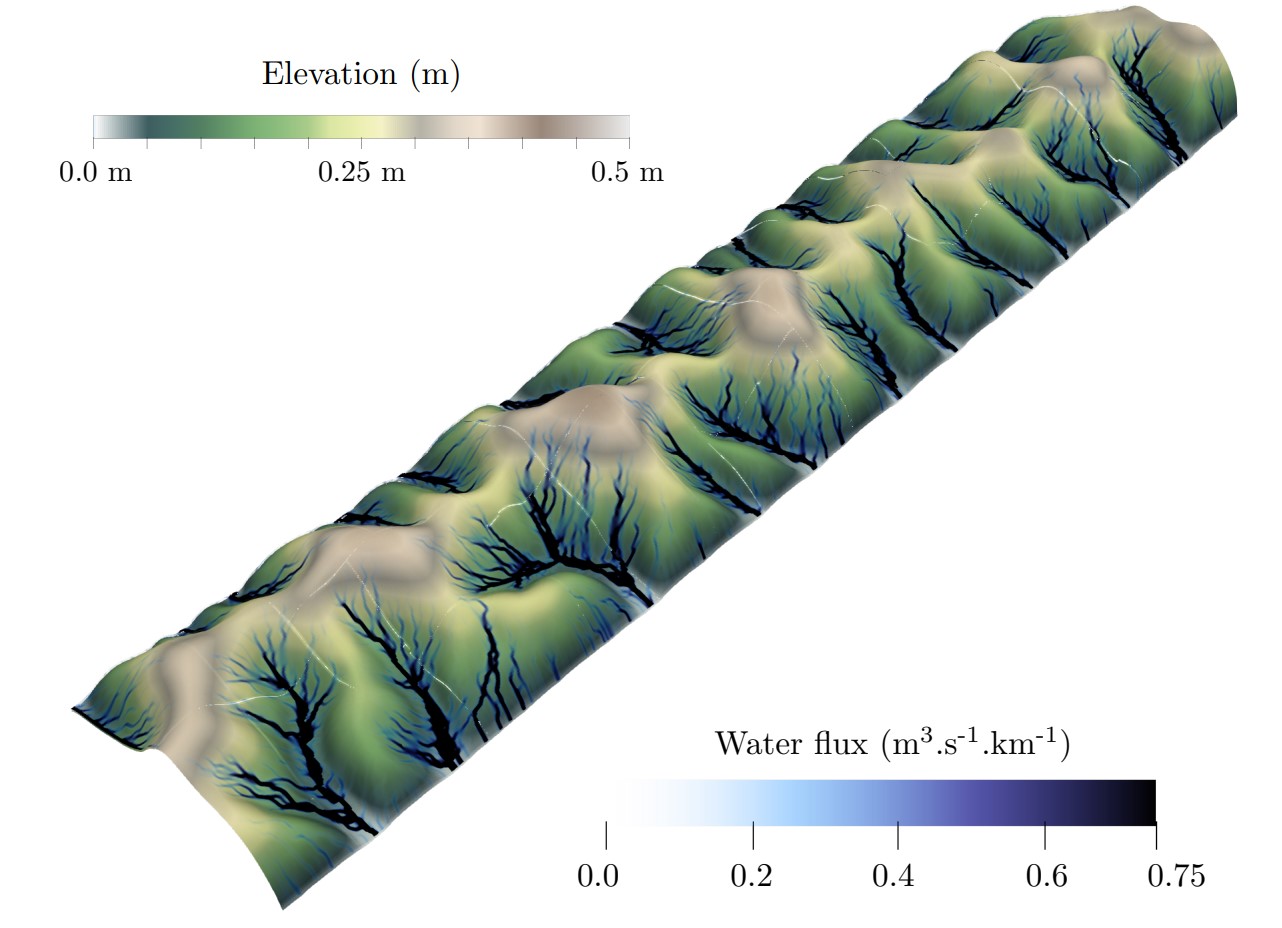
As with any good recipe, it is important to get the proportions right. And the same is true here, since the size of the filter to be chosen is governed by the size of the objects we want to preserve in our landscape. An object such as a mountain, a drainage basin or even a simple river should be approximately one order of magnitude larger than the size of the filter. As long as this rule is followed, all that's left to do is adapt the mesh size so that it can “capture” the filter correctly, and it’s ready!(Figure 2)

References :

[1] D. Granjeon (1996). Modélisation stratigraphique déterministe : Conception et applications d’un modèle diffusif 3-d multi-lithologique.(Deterministic stratigraphic modeling: Design and applications of a 3d multi-lithology diffusion model)  PhD thesis, Université de Rennes I

[2] J. Coatléven (2020). Some multiple flow direction algorithms for overland flow on general meshes, ESAIM: Mathematical Modelling and Numerical Analysis. 
      >> DOI: https://doi.org/10.1051/m2an/2020025

[3] J. Coatléven; B. Chauveau (2025). A post-processing solution to restore numerical consistency for classical flow routing algorithms. Computational Geosciences 
      >> DOI : https://doi.org/10.1007/s10596-025-10359-5

[4] J. Coatléven; B. Chauveau (2024). Large structure simulation for landscape evolution models, Earth Surface Dynamics. 
      >> DOI: https://doi.org/10.5194/esurf-12-995-2024 
 

Scientific contacts : Benoît Chauveau, Julien Coatléven