Machine learning accelerates access to high-precision data for chemistry via ab initio molecular dynamics

Ab initio calculations consist in solving the Schrödinger equation for a set of atoms representing a chemical system of interest. In chemical reactivity, ab initio molecular dynamics (AIMD) make it possible, for example, to predict rate constants with a high degree of accuracy, such as in the case of zeolites with protons as active sites. Nevertheless, the conditions for obtaining results with the required accuracy can involve excessive calculation times. A recently developed method (Machine Learning Perturbation Theory) makes it possible to overcome this obstacle. The chosen application is that of alkene isomerization and cracking in large-pore zeolites.

Ab initio calculations: perspectives and challenges

Ab initio calculations consist in solving the Schrödinger equation for a set of atoms representing a chemical system of interest. Solving the equation requires the use of varying degrees of approximation. The fewer these approximations are¹, the greater the accuracy of the calculation, but the higher the cost.
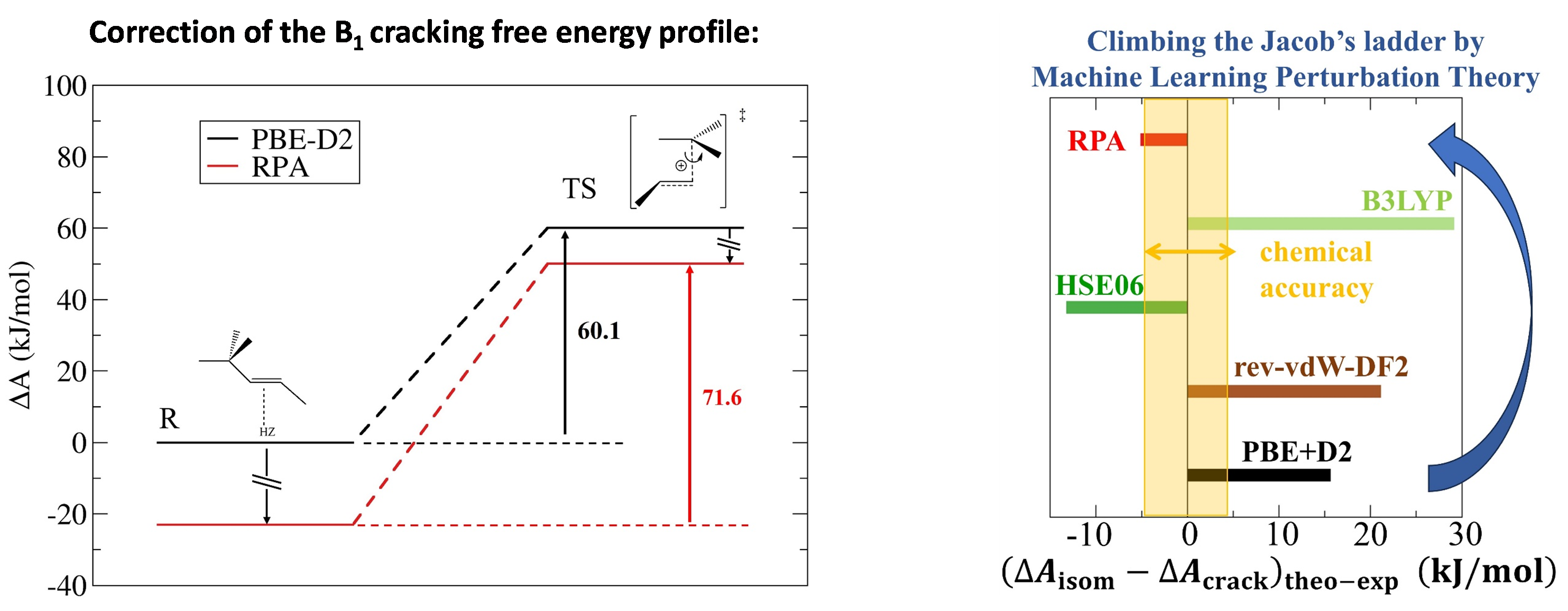
In the field of chemical reactivity, a major challenge for ab initio calculation is to be able to predict rate constants with an acceptable degree of accuracy². For some catalytic systems, such as zeolites with protons as active sites, this requires the use of a high level of theory and sampling of multiple configurations, for example via ab initio molecular dynamics (AIMD)³. Both of these aspects requires considerable computing resources to the point that, for calculations at the RPA (Random Phase Approximation)⁴ level , combining them should, in principle, lead to numerical resolution that could take around a millennium.

¹ This is known as “ high level of theory”
² Chemical accuracy with a deviation below 5 kJ/mol compared to reference experimental data 
³ In the case of a set of atoms, molecular dynamics consist in integrating equations of movement as a function of time, taking into account the effect of thermal agitation, with a chosen time step. Trajectories are thus obtained, making it possible to sample numerous system configurations (tens/hundreds of thousands). 
⁴ The RPA approach is used to solve the Schrödinger equation at a high level of theory and estimate the electronic correlation energy (interaction energy between electrons associated with their mutual influence). 

 
“Machine Learning Perturbation Theory”: a welcome ally

This major obstacle was recently overcome thanks to the implementation of the MLPT (Machine Learning Perturbation Theory) method, developed at Lorraine University and Bratislava University [1], and applied for the first time at such a high level of theory [2], for a rate constant calculation. The case of alkene isomerization and cracking in large-pore zeolites (Figure 1, left) was chosen in line with previous research. The AIMD calculation at the RPA level of theory was accelerated by a factor of 4,000. Moreover, this level appeared necessary (Figure 1, right) to achieve the expected accuracy, by comparison with experimental data acquired at IFPEN, and deciphered using kinetic modeling [3].

A ready-made future use: the conversion of bio-based molecules

This research, also highlighted in Science [4], paves the way for the near-chemically accurate prediction of rate constants for reactions of interest in numerous fields associated with new energy technologies. One example is the case of reactions involved in the conversion of bio-based molecules, such as alcohols and sugars. Hence, recent research conducted in partnership with Bratislava University has made it possible to:
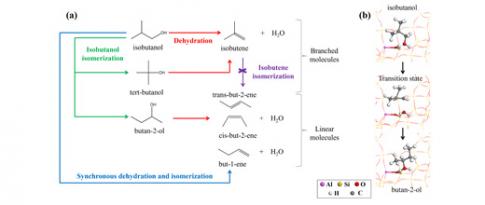
-    propose the first mechanisms capable of explaining the formation of linear butenes from isobutanol [5];
-    and, more recently, reveal the complexity of the reaction network by AIMD [6]. 

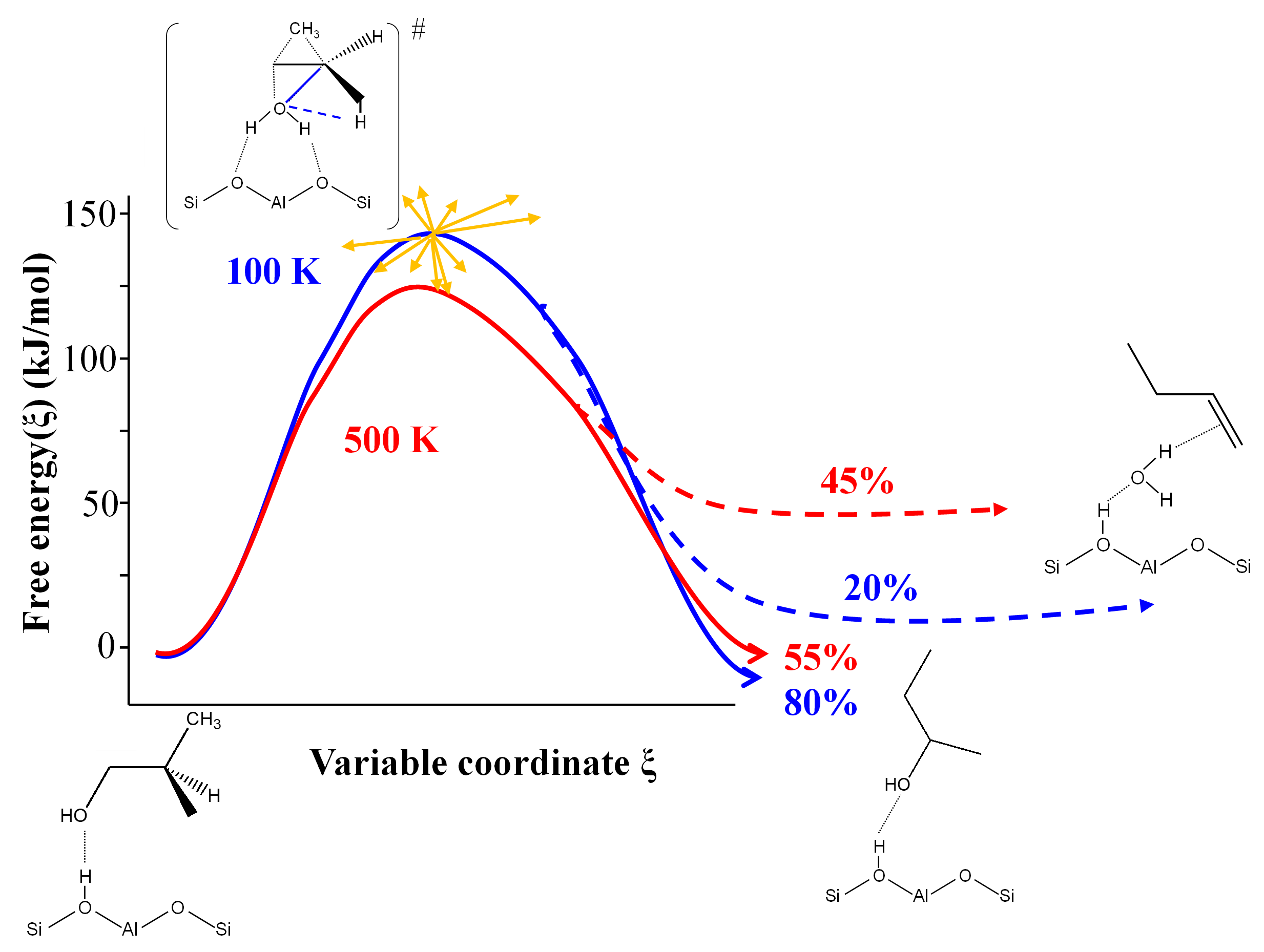
In the latter case, AIMD calculation demonstrates that several reactions enabling the formation of linear butenes share the same transition state, with a post-transition state bifurcation towards one product or another (Figure 2). For rate constant calculations, this prevents the traditional application of activated complex theory [7] and imposes the use of advanced AIMD methods.
The MLPT method will be used within the framework of the MAMABIO project (PEPR B-BEST) to improve the accuracy of these data relative to isobutanol dehydration.

References:

[1] Chehaibou, B.; Badawi, M.; Bucko, T.; Bazhirov, T.; Rocca, D., Computing RPA Adsorption Enthalpies by Machine Learning Thermodynamic Perturbation Theory, J. Chem. Theory Comput. 2019, 15, 6333-6342.

[2] Rey, J.; Chizallet, C.; Rocca, D.; Bučko, T.; Badawi, M., Reference-Quality Free Energy Barriers in Catalysis from Machine Learning Thermodynamic Perturbation Theory, Angew. Chem., Int. Ed 2024, 63, e202312392. Rey, J.; Badawi, M., Rocca, D., Chizallet, C., Bučko, T, Machine learning thermodynamic perturbation theory offers accurate activation free energies at the RPA level for alkene isomerization in zeolites, Catal. Sci. Technol., in press, 2024

[3] Schweitzer, J.-M.; Rey, J.; Bignaud, C.; Bučko, T.; Raybaud, P.; Moscovici-Mirande, M.; Portejoie, F.; James, C.; Bouchy, C.; Chizallet, C., Multiscale Modeling as a Tool for the Prediction of Catalytic Performances: The Case of n-Heptane Hydroconversion in a Large-Pore Zeolite, ACS Catal. 2022, 12, 1068-1081.

[4] Ash, C.; Smith, J.; Jiang, D.; McCartney, M.; Ross, S. H.; Maroso, M.; Nusinovich, Y.; Suleymanov, Y.; Wible, B., In Other Journals, Science 2024, 383, 380-381.

[5] Gešvandtnerová, M.; Bučko, T.; Raybaud, P.; Chizallet, C., Monomolecular mechanisms of isobutanol conversion to butenes catalyzed by acidic zeolites: Alcohol isomerization as a key to the production of linear butenes, J. Catal. 2022, 413, 786-802.

[6] Gešvandtnerová, M.; Raybaud, P.; Chizallet, C.; Bučko, T., Importance of Dynamic Effects in Isobutanol to Linear Butene Conversion Catalyzed by Acid Zeolites Assessed by AIMD, ACS Catal. 2024, 14, 7478-7491.

[7] Eyring, H., The Activated Complex in Chemical Reactions, J. Chem. Phys. 1935, 3, 107-115.
 

Scientific contact: Céline Chizallet