Thesis by Nicolas Fintzi, winner of the 2025 Yves Chauvin prize: « Modélisation statistique des écoulements à phases dispersées : application aux suspensions de gouttes entraînées par la flottabilité » (Statistical modeling of disperse two-phase flows : application to buoyancy-driven droplets suspensions).
Buoyancy-driven droplet flows are a type of two-phase flow found in many chemical engineering processes, such as gravity separators, liquid-liquid extractors, and flotation columns. It is essential to understand and model these flows in order to optimize the efficiency of the processes in question — for example, by improving phase separation and mass transfer.
The physical systems to be modeled cover a wide range of scales, from the size of droplets (a few micrometers) to that of industrial reactors (often more than a meter). With current computing resources, fully resolving all these scales through numerical simulation would require an excessively long computation time.
Hence, in order to describe the joint evolution of the dispersed phase (the droplets) and the continuous phase (the fluid surrounding the droplets), modern approaches rely on the use of averaged equations. These equations describe the average behavior of the two phases without requiring the complete resolution of the entire flow at local scales.
Furthermore, modeling of dispersed two-phase flows has historically primarily focused on suspensions of spherical solid particles and, to a lesser extent, on emulsions, where the dispersed phase is fluid. Yet, it is this latter situation, where the dispersed phase consists of fluid inclusions, that is found in many industrial and natural contexts (bubble flow, liquid-liquid mixtures, aerosols, etc.).
The main objective of this thesis was to construct a set of averaged equations capable of describing dispersed flows containing fluid inclusions. The dispersed phase was represented by averaged Lagrangian conservation laws, while the continuous phase was modeled by averaged Eulerian conservation laws (see [1]). This system is therefore referred to as a “hybrid model”.
A second aspect of this thesis was the development of closure models to feed into the equations of the “hybrid model” developed1.
1These “closure models” allow the flow behavior to be represented at scales not resolved by the averaged equations..
We then used the « Basilisk C » open-source code to perform numerical simulations of emulsions of droplets under gravity (see Figure 1), with the aim of accurately predicting their rheological behavior [2].
Our results, supplemented by theoretical analyses, show that it is essential to include the contribution of the relative velocity between phases, not only in the drag force — the average force exerted by the continuous phase on the droplets — but also in the effective stress2, including the effects of turbulent fluctuations.
2 Stress observed at macroscopic scale
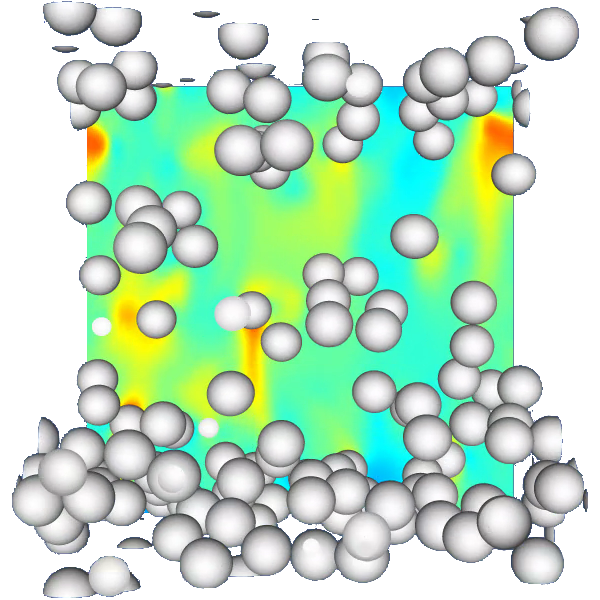
Lastly, this thesis also focused on the characterization of the microstructure of emulsions and the study of the relative kinematics of interacting droplets. To do this, we used the nearest neighbor pair distribution function, which describes the probability of finding two droplets at a given distance from one another.
This function was used to analyze the geometry of the microstructure, i.e., the way in which the droplets are organized in space.
We demonstrated that the standard deviation of this distribution is a good indicator for quantifying the formation of clusters, chains, or layers of droplets in the flow [3].
Finally, an equation describing the evolution (in time and space) of the standard deviation of this distribution was developed, enabling analysis of the kinematics of the emulsion microstructure. We showed that the average interaction time between droplets corresponds to the relaxation time3 of the standard deviation of the distribution of the closest pairs.
This characteristic time is thus a key parameter for describing the microstructure formation.
3 Time required for a system to return to equilibrium following a disturbance
This work establishes a solid general framework for future research on dispersed two-phase flows, taking into account, for example, coalescence, droplet deformation, or turbulence induced by droplet clusters, all phenomena that are still poorly understood yet essential for process modeling.
References:
- Fintzi, Nicolas, and Jean-Lou Pierson. "Averaged equations for disperse two-phase flow with interfacial transport." (Accepted: International Journal of multiphase flows)
>> arXiv preprint arXiv:2410.10752
- Fintzi, Nicolas, and Jean-Lou Pierson. " Averaged equations for suspensions made of slightly inertial buoyant spherical droplets." (submitted).
- Fintzi, Nicolas, Jean-Lou Pierson, and Stéphane Popinet. "Buoyancy driven motion of non-coalescing inertial drops: microstructure modeling with nearest particle statistics." Acta Mechanica (2024): 1-24.
Scientific contact: Nicolas Fintzi
You may also be interested in
