21.01.2021
4 minutes of reading
In order to reduce the calculation times previously required to optimize complex systems, such as electric machines or floating wind turbines, IFPEN’s researchers have explored new optimization solutions based on “Gaussian process” response surfaces with discrete variables. In particular, they have been able to reduce the number of simulations and achieve optimal results by using more efficient methods: EGO (Efficient Global Optimization) and MADS (Mesh Adaptive Direct Search).
The optimization of complex systems: a cost problem
The design of the complex systems developed by IFPEN (electric machines, floating wind turbines and their various components) involves solving optimization problems. Solving these problems may depend on discrete variables - such as, for example, a number of components (integer variables), different materials (categorical variables, generally unordered), the presence or otherwise of certain components (binary variables) - as well as continuous variables describing the dimensions or properties of the various components.
During their research, IFPEN’s teams turned their attention to so-called “engineering” models that, while being dependent on a limited number of variables of interest (typically fewer than 20), involve solving complex equations integrated in simulators that are costly in terms of calculation times (several hours of calculation time may be required to evaluate a single given configuration).
Reducing the number of simulations with the EGO method adapted to mixed variables
To solve this type of problem, IFPEN’s researchers focused on optimization methods based on “Gaussian-process” response surfaces, the variability of which is determined by the choice of a covariance function.
The advantage with these methods is that they are “economical”, since they require fewer simulations in order to approximate the optimal configuration. One example is the sequential EGO (Efficient Global Optimization) method, which was extended to the processing of “mixed variables”, i.e., where the vector of variables contains both continuous and discrete variables [1].
To achieve this, response surfaces were integrated with kernels making it possible to capture both the variability and correlations of the optimized function, on the basis of all the variables: continuous or discrete, in particular categorical.
MADS, a direct method in support of EGO method
There was a specific focus on solving the subproblems inherent to the EGO method associated with the choice of new simulations aimed at enriching the response surface. To this end, the direct MADS (Mesh Adaptive Direct Search) method was combined with a random exploration of the categorical variables space, based on a probability distribution obtained and updated as additional simulated data were acquired.
This approach, compared with state-of-the-art methods, proved its effectiveness, i.e., its capacity, firstly, to explore the field of categorical variables using fewer simulations (Figure) and, secondly, to obtain optimization results that are not sensitive to the choice of initial points.
Une attention particulière a été portée à la résolution des sous-problèmes de la méthode EGO qui sont associés au choix des nouvelles simulations destinées à enrichir la surface de réponse. A cette fin, la méthode directe MADS (Mesh Adaptive Direct Search) a été couplée avec une exploration aléatoire de l’espace des variables catégorielles, en se basant sur une distribution de probabilité apprise et mise à jour au fur et à mesure de l’acquisition de données simulées.
Cette approche, comparée à des méthodes de l’état de l’art, a démontré son efficacité, à savoir sa capacité à, d’une part, explorer le domaine des variables catégorielles en demandant moins de simulations (figure) et, d’autre part, obtenir des résultats d’optimisation peu sensibles au choix des points initiaux.
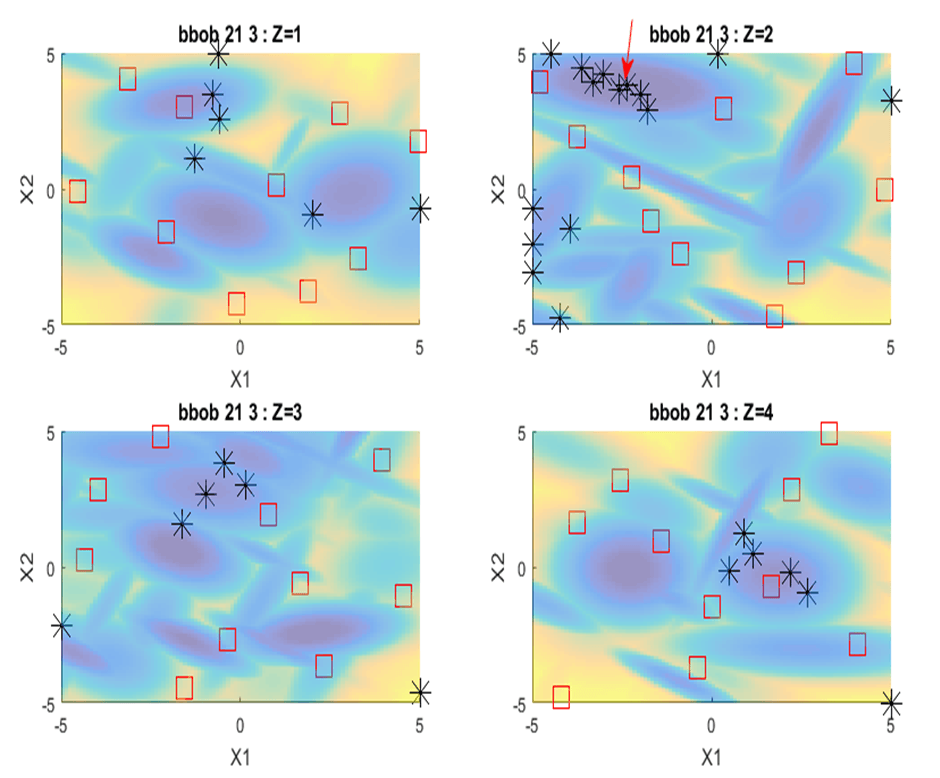
The colors indicate the levels of the function to be minimized (the red arrow indicates the location of the global optimum, associated with category 2). The red squares indicate the initial experimental design simulations and the black boxes the simulations added by the method.
This research work will be continued and supplemented by further approaches within the framework of new research initiatives, both internally at IFPEN [2] and as part of collaborative programs: with the support of the ANR [3], within a research consortium [4] and via a partnership with Polytechnique Montréal [5].
Références
[1] Munoz Zuniga M. and Sinoquet D., Global Optimization for mixed categorical-continuous variables based on Gaussian process models with a randomized categorical space exploration step, 2020, INFOR, Information Systems and Operational Research, https://doi.org/10.1080/03155986.2020.1730677
[2] DeTOCS project: DEsign Tools for Optimization and Control of complex Systems
[3] Samourai project(2021-2025) : "Simulation Analytics and Meta-model-based solutions for Optimization, Uncertainty and Reliability Analysis" with the CEA, Supelec, EDF, EMSE, IFPEN, Polytechnique Montréal, Safran.
[4] CIROQUO - “Consortium Industriel de Recherche en Optimisation et QUantification d'incertitudes pour les données Onéreuses” (industrial research consortium dedicated to the optimization and quantification of uncertainties for expensive data) - currently being set up by the Ecole Centrale Lyon and IFPEN, a follow-up to the OQUAIDO chair led by the Ecole des Mines engineering school in Saint Etienne (2016-2020).
[5] The “Variables de catégorie en optimisation de boîtes noires” (black-box optimization category variables) project led by S. Le Digabel (GERAD) and M. Munoz Zuniga (IFPEN) (2020-2021) and funded by the Samuel-De Champlain program within the framework of Quebec’s Nature et Technologies research fund.
Scientific contacts : Delphine Sinoquet - Miguel Munoz Zuniga






