08.12.2020
4 minutes of reading
Better predicting the retraction of a liquid ligament is useful both for IFPEN’s research activities and for studies on Covid transmission. Having concluded that the Taylor-Culick velocity was only valid to evaluate the characteristic retraction time for a liquid in an inertial regime, researchers at IFPEN have proposed a velocity that is valid in a viscous regime.
From COVID transmission to liquid jet atomization: where do droplets come into it?
The retraction of a liquid ligament is a generic process involved in numerous applications of interest to IFP Energies nouvelles, be it in the atomization of a liquid jet (engine application) or droplet fragmentation in turbulent flows (processes, water treatment).
The final mechanism driving droplet formation is generally the result of liquid ligament pinch-off [1], a problem also encountered in the COVID-19 pandemic in terms of virus transmission via saliva projections [2].
How can liquid retraction be predicted?
The principal challenge in all these applications is to predict whether the liquid will retract in a single spherical entity (its equilibrium shape) or break up into multiple droplets. A simple way of making such a prediction is to compare the characteristic ligament retraction time with the characteristic time for the appearance of capillary waves responsible for pinch-off (figure).
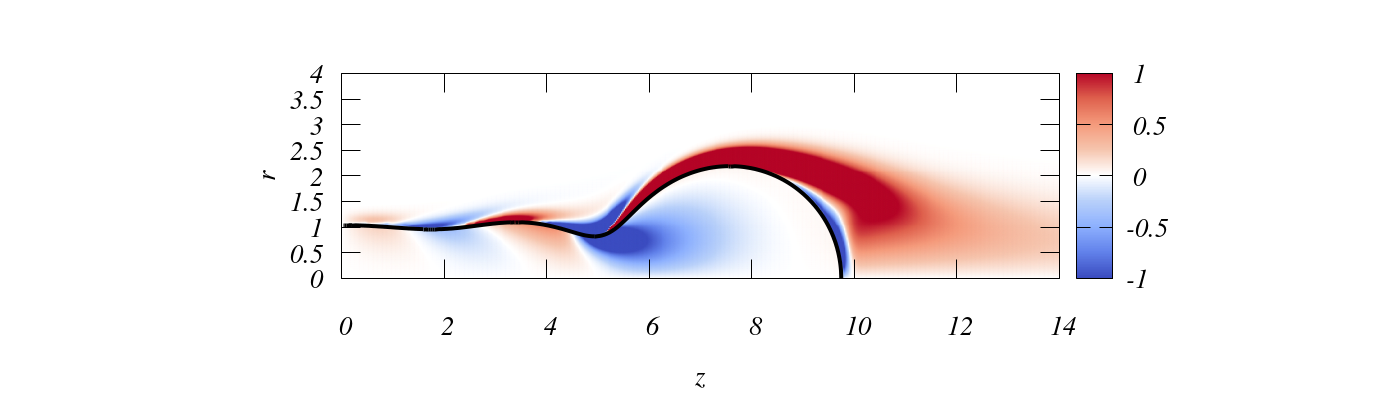
The Taylor-Culick velocity, its validity qualified by new research
Until very recently, the characteristic retraction time had been estimated via the so-called Taylor-Culick velocity [3,4], whether the liquid was highly viscous or, conversely, highly inertial. IFPEN conducted numerical and theoretical research, with contributions from a post-doctoral researcher and scientific visitor Professor Edson Soares, a specialist in fluid mechanics and the rheological characterization of complex fluids. The research demonstrated that this velocity was only valid in an inertial regime and for sufficiently long periods of time.
Viscous regimes: a decreasing retraction velocity over time
Researchers also proposed a self-similar solution - for which the shape of the droplet remains “similar” over time - in viscous regimes. This solution provides a retraction velocity that, unlike the Taylor-Culick velocity, is not constant but decreases over time. The ligament can then take an infinite amount of time to relax and return to its equilibrium position!
This research was the subject of two publications [5, 6] singled out in the editors’ selection.
Scientific contact : jean-lou.pierson@ifpen.fr
[1] Villermaux, E. (2020). Fragmentation versus cohesion. Journal of Fluid Mechanics, 898.
[2] Abkarian, M., & Stone, H. A. (2020). Stretching and break-up of saliva filaments during speech: A route for pathogen aerosolization and its potential mitigation. Physical Review Fluids, 5.
[3] Taylor, G. I. (1959). The dynamics of thin sheets of fluid. III. Disintegration of fluid sheets. Proceedings of the Royal Society of London. Series A. Mathematical and Physical Sciences, 253(1274), 313-321.
[4] Culick, F. E. C. (1960). Comments on a ruptured soap film. Journal of applied physics, 31(6), 1128-1129.
[5] Pierson, J. L., Magnaudet, J., Soares, E. J., & Popinet, S. (2020). Revisiting the Taylor-Culick approximation: Retraction of an axisymmetric filament. Physical Review Fluids, 5.
[6] Deka, H., & Pierson, J. L. (2020). Revisiting the Taylor-Culick approximation. II. Retraction of a viscous sheet. Physical Review Fluids, 5.





