In many geological reservoirs, pore size distribution is highly heterogeneous (from 2 to 50 nm). While the molecular size of the confined fluids is between 0.5 and 10 nm, their interaction forces with the micropore wall (~2 nm) are of the same order of magnitude as their intermolecular interactions, which can radically alter their thermodynamic behavior. Understanding this phenomenon is of significant interest to various industries: oil, chemicals, food, pharmaceutical, etc.
However, obtaining the required thermodynamic properties experimentallya remains technically challenging. Molecular simulation was recently employed at IFPEN to model phase equilibria in confined fluids. This alternative makes it possible to produce reference data for equations of state used in reservoir simulation.
A new Monte Carlo calculation methodb, with a modified version of the Gibbs ensemble, was used to obtain the thermodynamic properties at equilibrium of the confined mixtures and their liquid and vapour pressures(1).
The method was tested for pure hydrocarbons (C2, C5 and C10) and mixtures (C1/C2, C2/C5). Pores were modeled using slits with various sizes of graphite walls. Hydrocarbons were modeled with an anisotropic united atom potential, for different C2/C5 mixture proportions (figure). It is observed that the phase envelope of the confined fluid shifts and its size reduces. Simulations confirm that the critical temperature and pressure are shifted downwards and the bubble point pressure decreases while the dew point pressure increases.
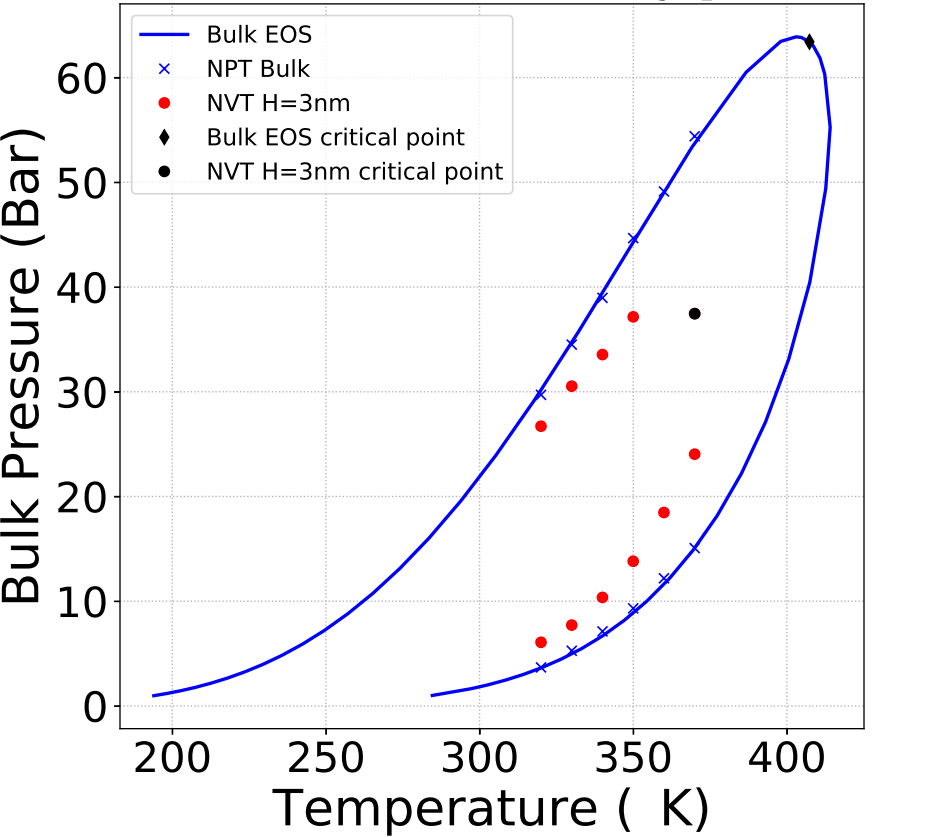
This information will be used to optimize the description of confined fluids via the calibration of equations of state.
a - Critical temperature, critical pressure and phase density.
b - Adaptation of the method fixing the bubble point pressure in order to initialize a constant temperature calculation.
c - The symbols represent simulation results while the continuous lines represent the results obtained from a cubic equation of state for unconfined fluids.
(1) N. Sobecki, C. Nieto-Draghi, A. Di Lella, D. Yu Ding, Phase behavior of hydrocarbons in nano-pores, Fluid Phase Equilibria (2019).
DOI: 10.1016/j.fluid.2019.05.025
Scientific contacts: Carlos Nieto - didier-yu.ding@ifpen.fr





