Dual-porosity and dual-fracture model for fractured geothermal reservoir simulation

Geothermal energy production has been developing since the start of the 2000s, and it is becoming necessary to have accurate numerical models to simulate the various scenarios that may be encountered. The dual-porosity model, which is widely used for flow simulations in “high-temperature” geothermal reservoirs, cannot correctly take into account certain phenomena such as thermal transfer and temperature change in fractured reservoirs. A new model combining dual-porosity and dual-fracture approaches is proposed here for a better description of these phenomena. The presented example is a reservoir represented by two orthogonal fracture networks in which water circulates between a horizontal injector and a horizontal producer.

The limits of the dual-porosity model

Currently, the dual-porosity model is widely used to simulate flows in so-called “high-temperature” geothermal reservoirs (deep reservoir with a temperature above 150°C), which are often naturally fractured. It is indeed well suited to situations where the convective flow, in fractures, is much faster than in the porous matrix. However, although this type of model is successfully used to simulate oil and gas reservoirs, it is less effective for geothermal reservoirs because thermal conduction plays a more significant role in this case and temperature variation is a major issue. A standard dual-porosity model assumes that pressure is locally constant in connected fractures, which is reasonable due to the high permeability in the fractures. But that is not the case for temperature, because thermal conductivity is as low in the fractured medium as it is in the porous matrix. Temperature diffusion is therefore much slower than pressure diffusion along the fractures. 

Extension of the dual-porosity model to a dual-fracture model

In order to improve the modeling of thermal transfer and temperature change for fractured geothermal reservoirs, the dual-porosity model was extended to a dual-fracture model [1]. 

In this model, the fractured medium is divided into two orthogonal fracture networks. They are hydraulically connected due to the high fracture permeability but there is little heat exchange between them due to the low thermal conductivity.

• Figure 1 gives an example of horizontal doublet (injection and production wells). Water at 80°C is injected into the geothermal reservoir of 200°C. The size of the matrix block in this reservoir is 100 m in the horizontal direction X and 25 m in the vertical direction Y.

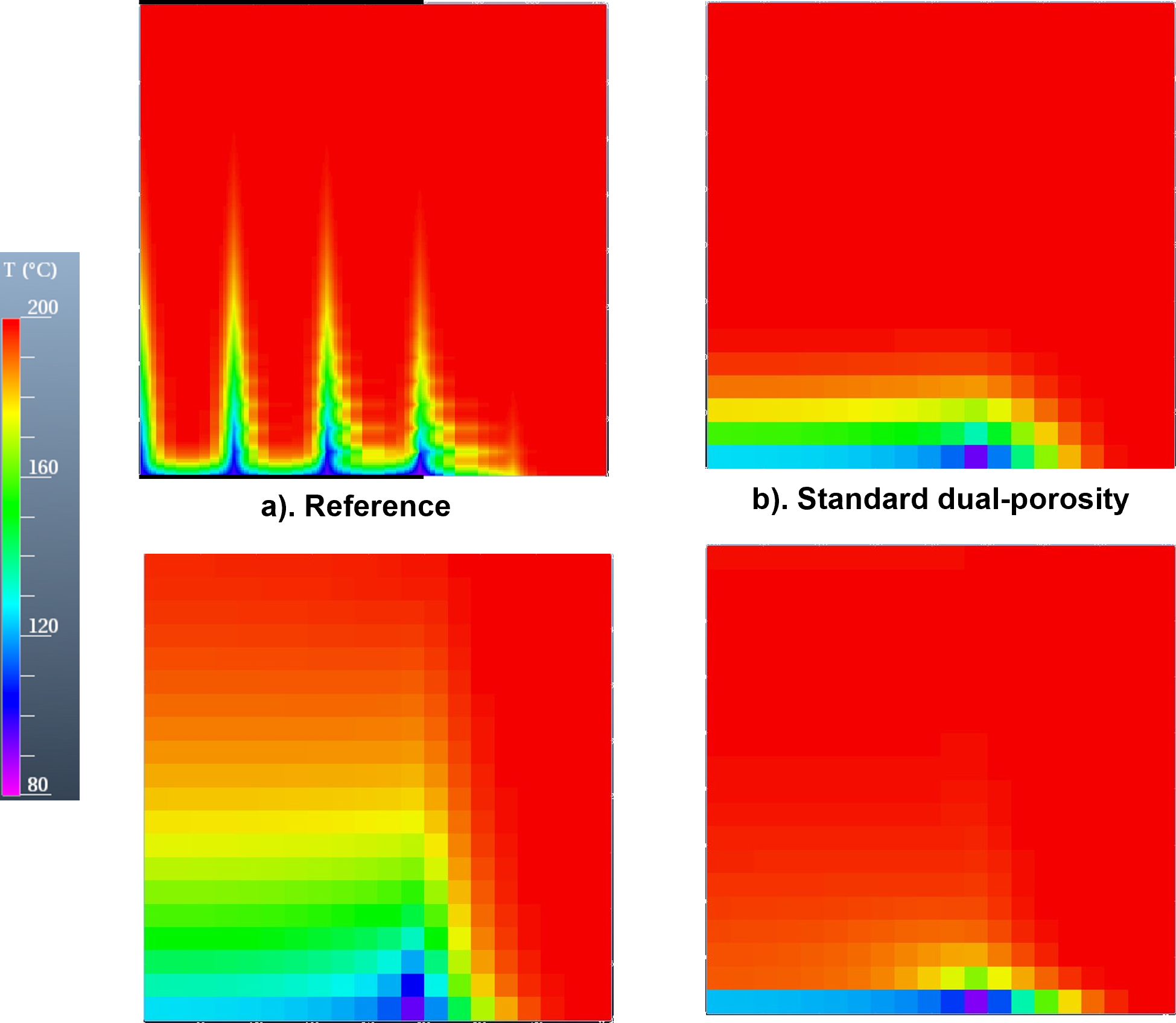
•  Figure 2 compares the temperature map in the reservoir after 1,000 days of injection, simulated with different models: a reference solution¹ (2a), the standard dual-porosity model (2b) and the dual-porosity/dual-fracture model (2c and 2d).With the reference solution (Figure 2a), the progress of the cold water front can be clearly seen in the Y direction, along the fractures connecting the geothermal doublet. This phenomenon cannot be reproduced with the standard dual-porosity model (Figure 2b). Using the dual-porosity/dual-fracture model, the cold water front moves quickly along the fracture network in the Y direction (Figure 2c), whereas the temperature in the fractures in the X direction spreads very slowly (Figure 2d), like the reference solution.

¹single-porosity model with very fine mesh and discretized fractures

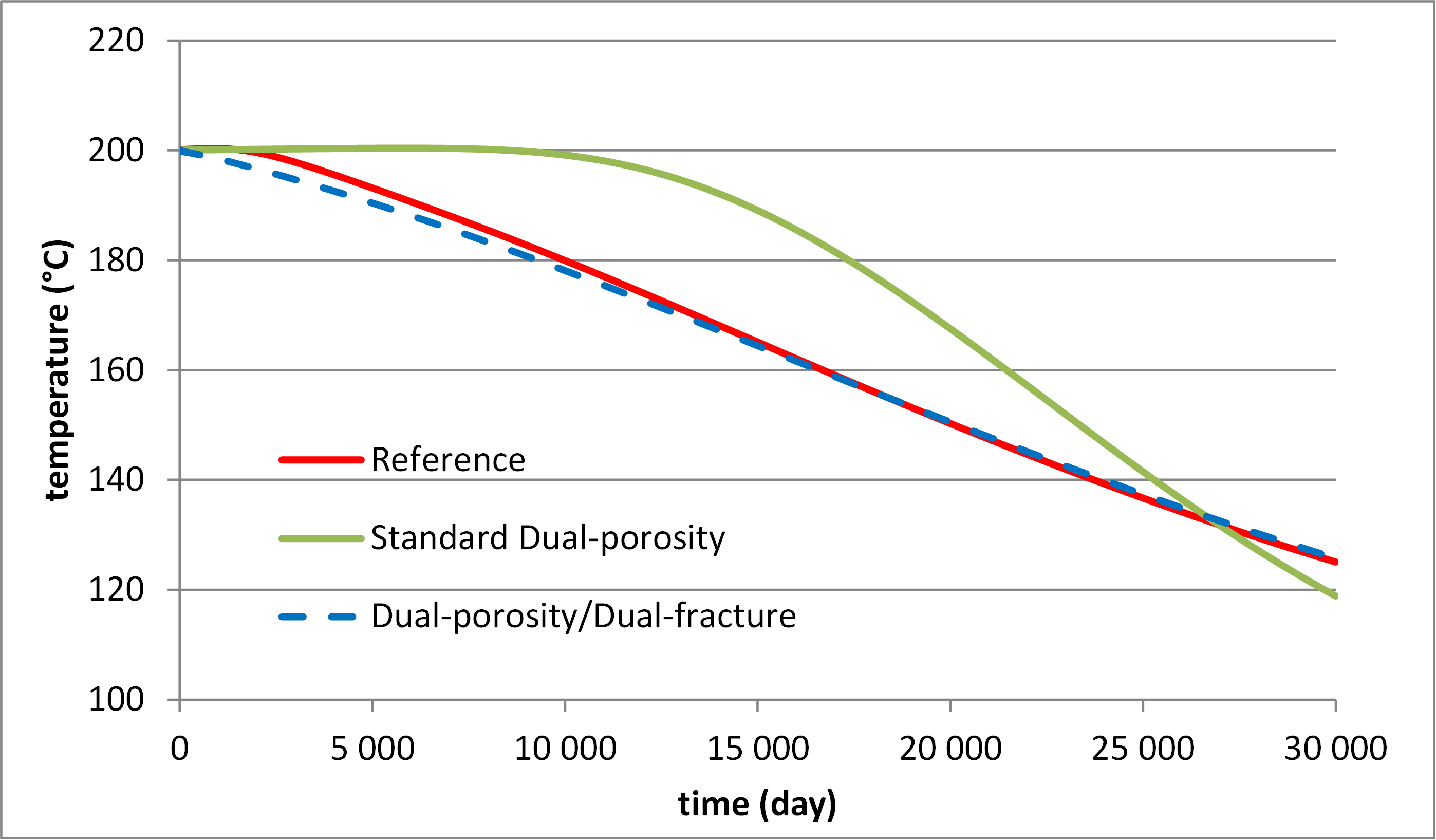
• Figure 3 shows that the evolution of the produced water temperature obtained via the dual-fracture model is very close to that of the reference solution, while it is not the case for the simulation with the standard dual-porosity model.

Dual-porosity/dual fracture: a realistic and extendible model 

This research showed that the dual-porosity/dual-fracture model is a realistic approach for fractured geothermal reservoir simulation with a good compromise in terms of accuracy and CPU time. 
Research will now focus on extending this type of simulation model to more realistic reservoir configurations, described by discrete fracture networks (DFN)².

² Discrete Fracture Networks : networks in which the geometric properties (for example, orientation, size, position, shape and aperture) of each individual fracture are explicitly represented, as well as the topological relationships between the fractures.

Reference :

[1] Ding, D.Y. (2022) “Dual-Porosity and Dual-Fracture Model for Fractured Geothermal Reservoir Simulations” Transp Porous Med 143, 169–194. https://doi.org/10.1007/s11242-022-01787-3
 

Scientific contact: Didier Y. Ding