Underground reservoir modeling in essential for many applications: aquifer management, underground compound or energy storage, mineral and energy resource recovery (e.g., geothermal energy). Modeling makes it possible to optimize resource management while minimizing societal and environmental risks. However, in order to be efficient, this modeling must be multiscale, and IFPEN’s research teams are therefore guided by this requirement.
Multiscale geoscience modeling
It is easy to understand the multiscale structure of the systems under consideration, for example by observing an underground outcrop, and then extrapolating the underlying underground structure. Observation, as well as drilling and detailed geological/geophysical analysis confirm the existence of embedded structures with scales varying from that of the pore, typically µm, to multi-kilometric scales. Geologists, geophysicists and petrophysicists are capable of providing relevant description tools for each of the scales considered, but they remain non-exhaustive.
Ideally, IFPEN’s geoscience specialists therefore have to construct models capable of reproducing this complexity, incorporating data observed at different scales, while at the same time taking into account the incomplete nature of the data.
Moreover, these researchers are quickly confronted with models with dozens of input parameters1. It is impossible to conduct a detailed exploration of a space of significant dimensions with existing or future calculation tools that soon come up against the “dimension wall”. It is this “wall” that justifies approaches such as “experimental design/model reduction” or recourse to artificial intelligence, which are associated with a considerable reduction in calculation cost, but ultimately rely on a very small learning base: at best a few thousand reference simulations to explore a space with thousands of dimensions.
A compromise is therefore to be found between these model reduction approaches and the need to maintain good physical coherence.
1 positions of limits, layer thicknesses, porosities, well positions and trajectories, injection and fluid production flows, etc
Multiscale geoscience modeling
Historically, the scale change idea precedes the approaches already outlined while complementing them. The idea is to reduce both the unit cost and the number of degrees of freedom describing the cumulated dimension of the parameters2. To do so, the description of the geological model is aggregated by grouping the parameters in order to construct a reduced model that is sufficient to reliably explore the configurations of interest. This approach is justified by the idea that the interest primarily lies in average values (fluid volumes, ore content, etc.) evaluated for the volume of the formation under consideration. This makes it possible to obtain an averaging effect similar to a law of large numbers smoothing out the details of the cases under consideration.
2 parameters qualified as controllable since they are reasonably known, or even chosen (well position, extraction flows) or said to be “uncontrollable” since they are imposed by nature, and therefore known with a degree of uncertainty.
Research conducted
The approach adopted consisted in tackling a model flow problem in porous media combining deterministic scaling with a stochastic approach. This involved analyzing simulation results while arbitrarily drawing several “geological reality” scenarios represented in the form of a random permeability map using artificially generated structures. This research was reported in the articles referenced below. Some of the principal elements are described here.
Figure 1 illustrates the typical geometry of the simulation of a flow problem in porous media. The real geometry is “meshed” by a fine grid incorporating the details of the form of the boundaries and discontinuities of the domain, and each mesh is described by a set of parameters derived from geological data (porosity, permeability, etc.). An intermediate calculation scale is then used to obtain reliable results, i.e., without any significant degradation in the quality of discontinuity representation or that of geological data. This optimal quality-cost compromise can be determined by establishing the characteristic spatial scales of the solutions to the simplified problem.
The approach adopted consisted in tackling a model flow problem in porous media combining deterministic scaling with a stochastic approach. This involved analyzing simulation results while arbitrarily drawing several “geological reality” scenarios represented in the form of a random permeability map using artificially generated structures. This research was reported in the articles referenced below. Some of the principal elements are described here.
Figure 2 illustrates the post-treatment results obtained via a rapid resolution of the flow for a random medium. The histograms of the permeability distributions obtained via post-treatment of the solution at different scales are shown on the figure on the right. Convergence of the distributions towards the Gaussian distribution illustrates the role of the size of the representative elementary volume. It can be noted that convergence toward a limiting distribution is slower when a bimodal permeability distribution is taken into account. At the connectivity (percolation) threshold, the bimodal character persists on a large scale and convergence towards “the equivalent homogeneous” becomes very slow, since the medium can hardly be homogenized anymore.
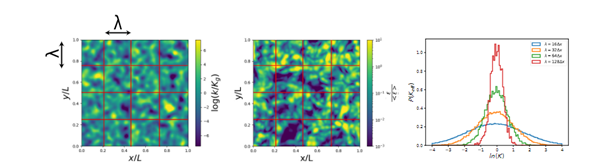
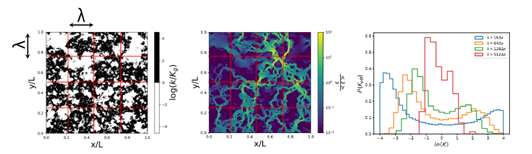
Figure 3 presents the permeability variance evolution (in Log) as a function of the distance to the percolation threshold, for various discrete image generation techniques (bottom of figure 2). The grouping of the curves can make it possible to rapidly anticipate the macroscopic flow regime for a specific case, and the relevant scales of a problem.
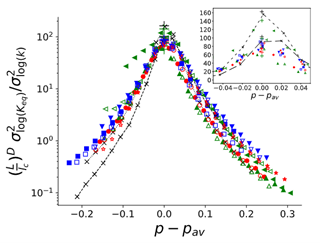
The results of this research provide a better understanding of the scaling process through the sparing (post-treatment) use of simulation results. By using this method, during the calculation process it becomes possible to identify relevant scales and parameter aggregates controlling end results of interest for applications. In particular, approaches of this type will be put to good use in the ERC Karst project.
References:
[1] Colecchio, I., Boschan, A., Otero, A. D., & Noetinger, B. (2020). On the multiscale characterization of effective hydraulic conductivity in random heterogeneous media: a historical survey and some new perspectives. Advances in Water Resources, 140, 103594, https://doi.org/10.1016/j.advwatres.2020.103594.
[2] Noetinger, B. (2020). Statistical physics and applied geosciences: some results and perspectives. Comptes Rendus. Physique, 21(6), 539-560, DOI:10.5802/crphys.40.
[3] Colecchio, I., Otero, A. D., Noetinger, B., & Boschan, A. (2021). Equivalent hydraulic conductivity, connectivity and percolation in 2D and 3D random binary media. Advances in Water Resources, 158, 104040, https://doi.org/10.1016/j.advwatres.2021.104040.
Scientific contact : B. Noetinger
You may also be interested in
KARST research project : IFPEN recipient of an ERC Synergy Grant
Karst aquifers: IFPEN launches a research project in hydrogeology
