The design of high-quality porous materials is a major challenge for the energy efficiency of industrial processes in the fields of catalysis and biocatalysis and separation and purification operations. For such applications, these materials derive their properties of interest from their specific microstructure, incorporating a large quantity of empty spaces that are organized and connected on a nanometric scale. IFPEN and Saint Gobain Research Provence (SGRP) joined forces to acquire a tool that will ultimately facilitate the development of porous materials optimized for given usages1. The partners adopted an innovative approach based on digital twins, developed from random microstructure models and adjusted using numerical models that imitate experimental procedures. This approach was then validated by comparison with test results on model microstructures.
Numerical simulation of experimental aspects is conducted on simulated three-dimensional microstructures [1] and is based on a geometric approach. Hence the approach adopted primarily uses correlations between the morphological parameters and physical quantities that characterize the system under consideration. It is this transition from a description of quasi-static states of physicochemical mechanisms - such as phase equilibrium changes - to the purely geometric and morphological description of the phenomena at play that represents the biggest difficulty to be overcome.
Mathematical morphology, a scientific field that has long focused on the characterization of the 2D and 3D textural properties of microstructures, proved invaluable to the resolution of this challenge. To construct the digital material, specific pore network extraction algorithms [2] firstly made it possible to consider pores with complex and random geometries, similar to those encountered in real materials (figure). Mathematical morphology operators2 were then used to simulate the phenomena involved in experimental porosimetry techniques. In particular, an operator of interest for these porous networks was estimated: tortuosity (figure), a property closely related to diffusion phenomena since it characterizes ease of flow across these networks [3].
With this type of digital twin approach, experimental simulations can take into account large representative volumes, with multi-scale and multi-structure arrangements, with reasonable calculation times.
In order to further optimize calculation time without compromising the precision of results, deep learning is a promising tool currently being evaluated to establish a direct link between digitized microstructures and simulated test results.
Click on the picture to enlarge
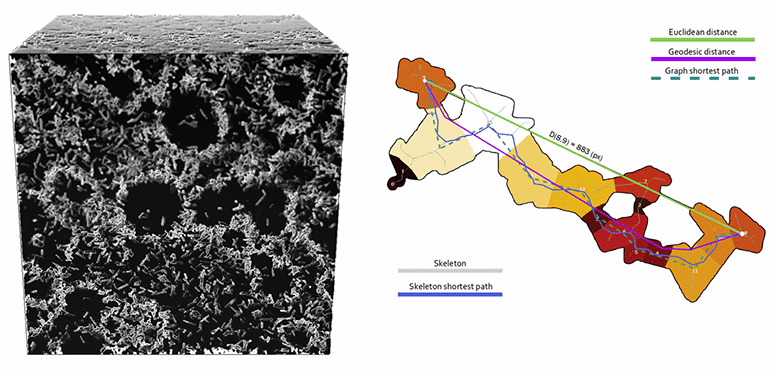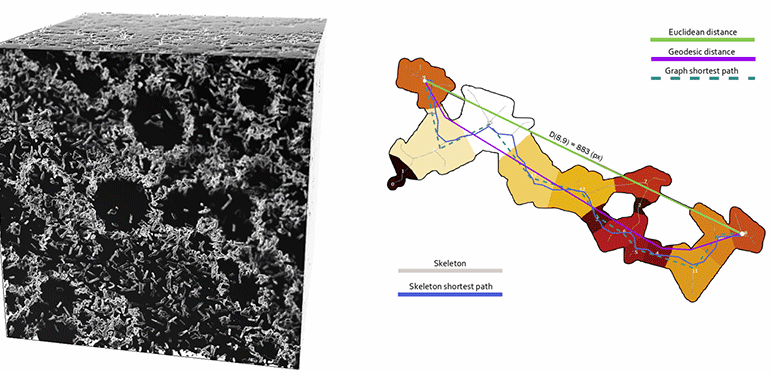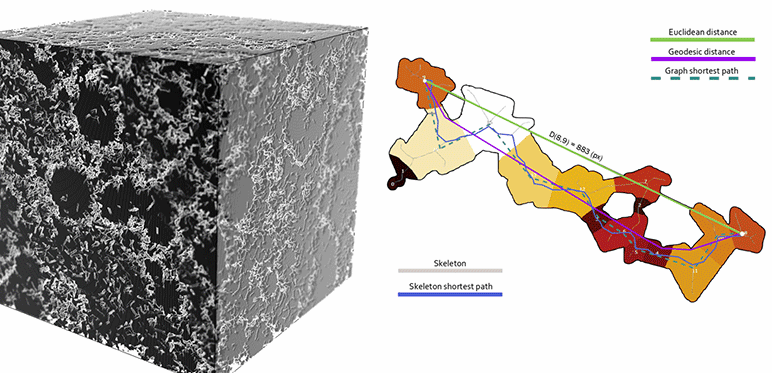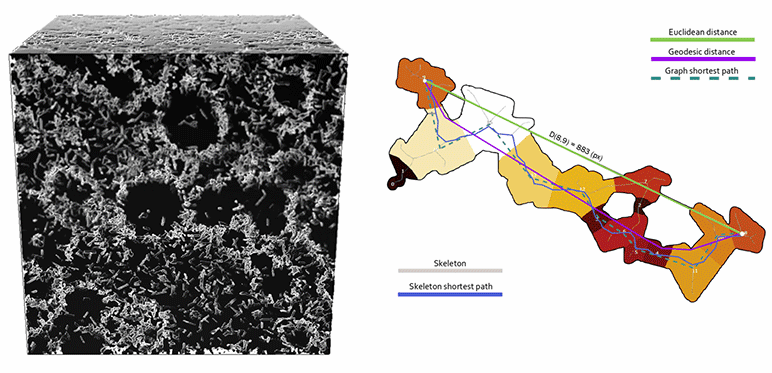
On the right, illustration of a tortuosity operator, ratio of the lengths of paths between two points “as the crow flies” (Euclidean distance) and constrained by the porous network (geodesic distance).
1- This research, launched in 2019, has been the focus of post-doctoral work conducted by Alexey Novikov and the PhD thesis research currently being conducted by Adam Hammoumi.
2-See examples at https://fr.wikipedia.org/wiki/Morphologie_math%C3%A9matique
Publications:
[1] M. Moreaud, J. Chaniot, T. Fournel, J.M. Becker, L. Sorbier. Multi-scale stochastic morphological models for 3D complex microstructures. 17th Workshop on Information Optics (WIO), IEEE Conference (2018).
>> https://doi.org/10.1109/WIO.2018.8643455
[2] A. Hammoumi, M. Moreaud, E. Jolimaitre, T. Chevalier, A. Novikov, M. Klotz. Efficient Pore Network Extraction Method Based on the Distance Transform. International Conference on Artificial Intelligence & Industrial Applications. Springer Ed. (2020).
>> https://doi.org/10.1007/978-3-030-53970-2_1
[3] A. Hammoumi, M. Moreaud, E. Jolimaitre, T. Chevalier, A. Novikov, M. Klotz. Graph-based M-tortuosity estimation. IAPR International Conference on Discrete Geometry and Mathematical Morphology (2021).
Scientific contact: Maxime Moreaud





